Componente fundamentale
- Tipuri
- Conversia Analog Digitala
- Codarea surselor
- Anlogice (continue)
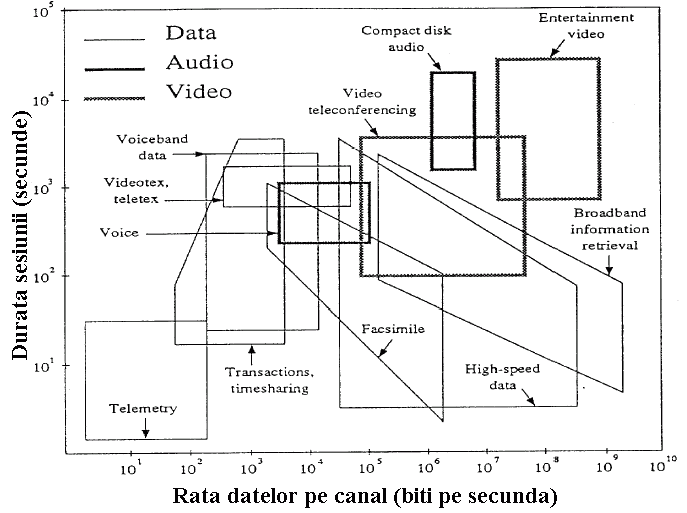
- voce, audio, imagine, video
- Latime de banda - gama de frecvente
- Statistici - distributie, putere, spectru
- Digitale
- Esantioane de date, date provenind de la calculatoare
- Rata de biti (bit rate): bps, kbps, Mbps, Gbps, Tbps
- Proces in doua etape
- Esantionare
- Teorema esantionarii
- Frecventa Nyquist
- Cuantizare
- Precizie, SNR (Signal to Noise Ratio)
Toate semnalele pot fi reprezentate prin colectii de numere oricat de acurate
rezultate in urma procesului de esantionare care produce numere reprezentand
valori ale semnalului la anumite momente de timp.
Teorema esantionarii a lui Shannon afirma ca:
- orice semnal de banda limitata poate fi reprezentat prin esantioane
prelevate la o frecventa egala cu dublul frecventei maxime* din spectrul
semnalului
- poate fi reconstruita fara erori daca sunt folosite functii de interpolare
adecvate**.
* dublul frecventei maxime a unui semnal este numita frecventa Nyquist.
** functia nerealizabila fizic sinx/x (sinc).
Teorema de esantionare a lui Shannon afirma ca orice functie (semnal) de
banda strict limitata poate fi reprezentat prin esantioanele sale luate la o
frecventa de cel putin dublul celei mai mari frecvente din spectrul semnalului.
Mai mult ea afirma ca functia originala poate fi restaurata fara distorsiuni
prin trecerea esantioanelor (pulsurilor) printr-un filtru trece-jos ideal cu
banda egala cu cea a semnalului.
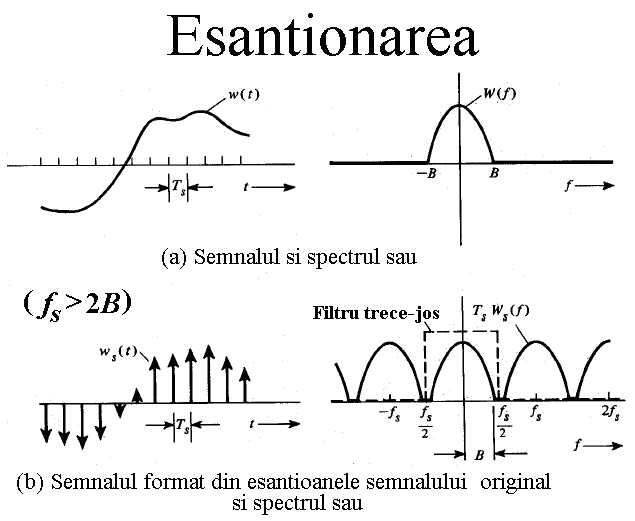

Orice semnala de banda strict limitata poate fi
reprezentat - exact - prin esantioanle luate la intervale de timp egale.
- De fapt, printr-un numar finit de esantioane prelevate la o frecventa de
doua ori mai mare decat latimea de banda.
- Totusi, functii de interpolare ideale (nerealizabile fizic) sunt necesare
pentru a reconstrui fara distorsiuni functia originala.
- Pentru procesare, memorare sau transmisie, esantioanle cu precizie
infinita trebuie cuantizate.
- Astfel, o gama (un interval) de valori este reprezentata printr-un singur
numar cu precizie finita. Spre exemplu, reprezentandu-le prin numere binare
finite.
- Eroarea de cuantizare depinde de numarul de intervale de cuantizare
utilizat.
- daca sunt folositi pentru reprezentare numere binare de N biti, numarul de
intervale distincte este 2N.
- Raportul semnal/eroare-de-cuantizare este de aproximativ 6N dB.
(Intr-adevar, 20·log(2N/1) ~ 6N dB)
- Definitia informatiei
- Conceptul de entropie a comunicatiei (informatiei)
- Teorema codarii sursei
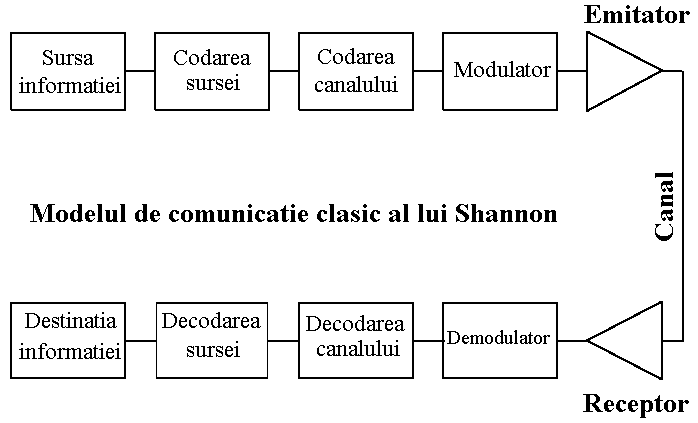
- Shannon a definit informatia generata de aparitia unui simbol xi
la iesirea unei surse discrete (care emite simboluri in numar finit) X prin
I(xi) = -log2{p(xi)*} = log2{1/p(xi)}
biti
- Aceasta masura este numita self-informatie a lui xi.
- Cu cat este mai putin probabila aparitia unui simbol - cu atat sursa
genereaza mai multa informatie prin emiterea acelui simbol;
*p(xi) este probabilitatea cu care sursa discreta X emite
simbolul xi.
- Shannon a definit entropia unei sursei discrete X self-informatia
medie H(X) a acesteia.
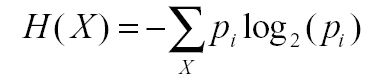
- Cu cat este mai mare entropia unei surse, cu atat este mai putin
predictibila aparitia unui simbol al sau.
- O sursa are entropia maxima atunci cand toate simbolurile au aceeasi
probabilitate de aparitie. Nu exista nici o modalitate de a le distinge a
priori.
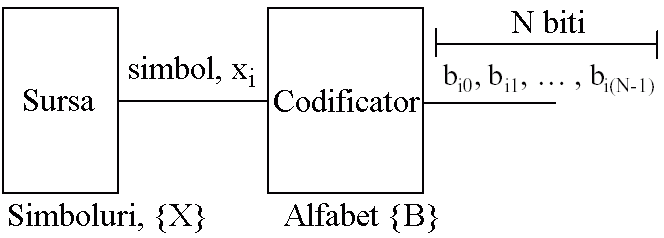
Idea codarii sursei este de a reprezenta fiecare aparitie a unui simbol
printrun sir de simboluri alese dintr-un alfabet, B. In exemplul de mai sus,
simboluri de la sursa discreta X (dintre care M sunt simboluri distincte) sunt
reprezentate printr-un cuvant de cod din N simboluri alese dintr-un alfabet B
care are K simboluri distincte. Intr-un exemplu simplu, sa consideram sursa un
convertor A/D cu 256 niveluri de cuantizare si fie B un alfabet binar cu K=2
simboluri. Daca sursa emite simbolurile sale echiprobabil, N trebuie sa fie 8
pentru a reprezenta numerele de la iesirea convertorului. Daca nivelurile nu
sunt echiprobabile, atunci putem utiliza coduri cu lungime variabila in care
anumite coduri vor fi reprezentate prin mai putin de 8 biti iar altele prin mai
mult de 8 biti. Putem face asta astfel incat lungimea medie a codului sa fie mai
mica de 8 biti.
Simbolurile emise de o sursa discreta pot fi reprezentate prin cuvinte in cod
binar a caror lungime medie L este marginita de entropia sursei si
entropia sursei plus 1 (in biti),
adica
H(X) < L < H(X) + 1
- Semnificatia teoremei codarii sursei este ca exista o cantitate de
informatie care este suficienta pentru a reprezenta o sursa.
- Corolarul este ca aceasta cantitate de informatie este si necesara pentru
a reprezenta o sursa.
- Daca o sursa este reprezentata prin mai putini biti decat entropia sa, va
exista cu certitudine o pierdere de fidelitate.
- Cele mai multe surse au semnalele de iesire redundante, astfel incat pot
fi comprimate, prin eliminarea redundantelor.
- Compresia poate fi cu sau fara pierderi.
- Acuratetea reprezentarii prin esantionare, cuantizare si compresie
este definita intotdeauna relativ la un criteriu de fidelitate.
- Gradul de compresie depinde de
- distributia de probabilitate a semnalului de iesire
- criteriul de fidelitate aplicat
Lungimea cuvantulul de cod a codului Huffman urmator este 2.63 biti. Daca
simbolurile sursei ar fi fost echiprobabile, cuvintele de cod ar fi avut
lungimea de 3.00 biti.
| i |
p(xi) |
Cod |
| 0 |
0.30 |
00 |
| 1 |
0.25 |
10 |
| 2 |
0.15 |
010 |
| 3 |
0.10 |
110 |
| 4 |
0.08 |
111 |
| 5 |
0.06 |
0110 |
| 6 |
0.04 |
01110 |
| 7 |
0.02 |
01111 |
Pentru acelasi cod, un script din pagina, calculeaza entropia si
media numarului de biti transmisi de aceasta sursa:
In cazul in care simbolurile ar fi echiprobabile
(adica p(xi) = 1/8) si nu s-ar folosi coduri de lungime fixa 3 biti
s-ar obtine pentru codul Hoffman de mai sus o lungime de cuvant medie:
© Cornel Mironel Niculae, 2004-2005
25-Mar-2008





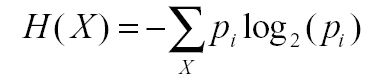

![]()